陕西省2023年秋季学期高一期中考试（241224Z）数学试卷答案,我们目前收集并整理关于陕西省2023年秋季学期高一期中考试（241224Z）数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

陕西省2023年秋季学期高一期中考试（241224Z）数学试卷答案

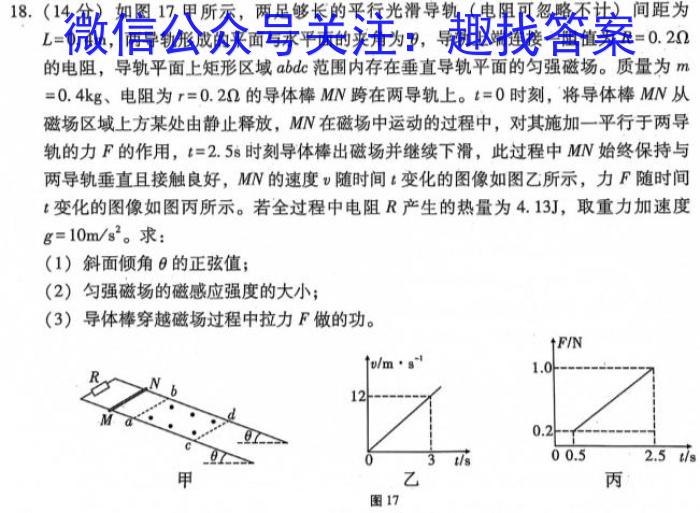
18.(14分)如图17甲所示,两足够长的平行光滑导轨(电阻可忽略不计)间距为L=0.4m,,两导轨形成的平面与水平面的夹角为θ,,导轨上端连接一阻值为R=0.2Ω的电阻,导轨平面上矩形区域abd范围内存在垂直导轨平面的匀强磁场。质量为m=0.4kg、、电阻为r=0.2Ω的导体棒MN跨在两导轨上。t=0时刻,将导体棒MN从磁场区域上方某处由静止释放,MN在磁场中运动的过程中,对其施加一平行于两导轨的力F的作用,t=2.5g时刻导体棒出磁场并继续下滑,此过程中MN始终保持与两导轨垂直且接触良好,MN的速度v随时间t变化的图像如图乙所示,力F随时间t变化的图像如图丙所示。若全过程中电阻R产生的热量为4.13J,取重力加速度g=10m/s^2。,求:(1)斜面倾角θ的正弦值;(2)匀强磁场的磁感应强度的大小;(3)导体棒穿越磁场过程中拉力F做的功。tF/N

分析（1）①要判断函数g（x）=2^x-1，（x∈[0，1]）在区间[0，1]上是否为“理想函数，只要检验函数g（x）=2^x-1，是否满足理想函数的三个条件即可；
（2）先研究函数f（x）的单调性，从而得出此函数的最值．得到当x=0时，f（x）取得最小值2，当x=1时，f（x）取得最大值3即可；
（3）由条件③知，任给m、n∈[0，1]，当m＜n时，由m＜n知n-m∈[0，1]，f（n）=f（n-m+m）≥f（n-m）+f（m）≥f（m）．由此能够推导出f（x₀）=x₀．，根据f[f（x₀）]=x₀，则f（x₀）=x₀．

解答解：（1）①显然f（x）=2^x-1在[0，1]上满足f（x）≥0；②f（1）=1．
若x₁≥0，x₂≥0，且x₁+x₂≤1，
则有f（x₁+x₂）-[f（x₁）+f（x₂）]=2^x₁+x₂-1-[（2^x₁-1）+（2^x₂-1）]=（2^x₂-1）（2^x₁-1）≥0
故f（x）=2^x-1满足条件①②③，所以f（x）=2^x-1为理想函数，
（2）设x₁，x₂∈[0，1]，x₁＜x₂，则x₂-x₁∈（0，1]
∴f（x₂）=f[（x₂-x₁）+x₁]≥f（x₂-x₁）+f（x₁）-2
∴f（x₂）-f（x₁）≥f（x₂-x₁）-2≥0，
∴f（x₁）≤f（x₂），则当0≤x≤1时，f（0）≤f（x）≤f（1），
在③中，令x₁=x₂=0，得f（0）≤2，由②得f（0）≥2，
∴f（0）=2当x=1时，f（1）=3，
∴当x=0时，f（x）取得最小值2，
当x=1时，f（x）取得最大值3，
（3）由条件③知，任给m、n∈[0，1]，当m＜n时，由m＜n知n-m∈[0，1]，
∴f（n）=f（n-m+m）≥f（n-m）+f（m）≥f（m）．
若f（x₀）＞x₀，则f（x₀）≤f[f（x₀）]=x₀，前后矛盾；
若：f（x₀）＜x₀，则f（x₀）≥f[f（x₀）]=x₀，前后矛盾．
故f（x₀）=x₀．

点评赋值法是解决抽象函数问题的常用方法，函数的新定义则转化为函数性质问题，本题则结合指数函数的性质，探讨函数的函数值域，指数函数的单调性的应用等知识点．