2024届高三第三次大联考试卷（XGK）数学试卷答案,我们目前收集并整理关于2024届高三第三次大联考试卷（XGK）数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

2024届高三第三次大联考试卷（XGK）数学试卷答案

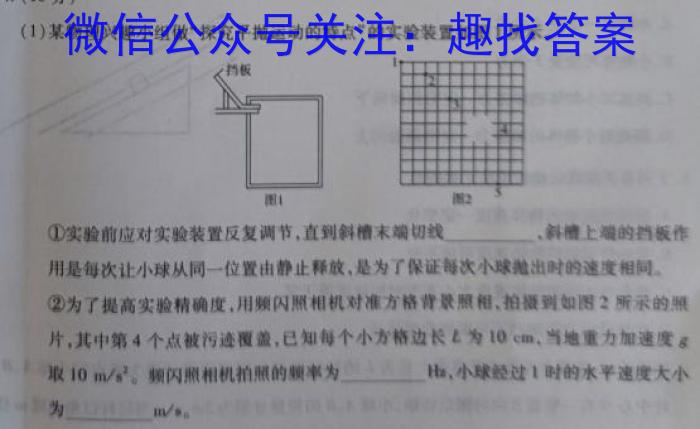
(1)某物理兴趣小组做“探究平抛运动的特点”的实验装置如图1所示。①实验前应对实验装置反复调节,直到斜槽末端切线、斜槽上端的挡板作用是每次让小球从同一位置由静止释放,是为了保证每次小球抛出时的速度相同。②为了提高实验精确度,用频闪照相机对准方格背景照相,拍摄到如图2所示的照片,其中第4个点被污迹覆盖,已知每个小方格边长L为10cm,当地重力加速度g取10m/s^2。。频闪照相机拍照的频率为,小球经过1时的水平速度大小为m/s0

分析由题意转化为在x∈[-1，1]上，f（x）_max-f（x）_min≥$\frac{a+1}{2}$，即原题函数模型变为g（t）=at+$\frac{1-a}{t}$-2，t∈[$\frac{1}{2}$，2]，分类讨论，利用函数的单调性，即可求出a的范围．

解答解：首先存在x₁，x₂∈[-1，1]使得$|{f（{x_1}）-f（{x_2}）}|≥\frac{a+1}{2}$成立的意思是：
在x∈[-1，1]上，f（x）_max-f（x）_min≥$\frac{a+1}{2}$，
f（x）=$\frac{a•{4}^{x}-{2}^{x+1}-a+1}{{2}^{x}}$=a•2x+$\frac{1-a}{{2}^{x}}$-2
令$t={2^x}∈[{\frac{1}{2}，2}]$，原题函数模型变为g（t）=at+$\frac{1-a}{t}$-2，t∈[$\frac{1}{2}$，2]，
1°当a≤0时，g（t）在$t∈[{\frac{1}{2}，2}]$单调递减，所以$g{（t）_{max}}-g{（t）_{min}}≥\frac{a+1}{2}$
等价于$g（{\frac{1}{2}}）-g（2）≥\frac{a+1}{2}⇒a≤\frac{2}{7}$，所以a≤0
2°当0＜a＜1时，$g（t）=a（{t+\frac{{\frac{1-a}{a}}}{t}}）-2$，
g（t）在$（{0，\sqrt{\frac{1-a}{a}}}]$上单调递减，在$[{\sqrt{\frac{1-a}{a}}，+∞}）$上单调递增
所以需要比较$\sqrt{\frac{1-a}{a}}$的位置与$[{\frac{1}{2}，2}]$的关系，从而得到分类标准：
①$\sqrt{\frac{1-a}{a}}≤\frac{1}{2}$时，$\frac{4}{5}≤a＜1$时，g（t）在$[{\frac{1}{2}，2}]$单调递增，
∵$g{（t）_{max}}-g{（t）_{min}}≥\frac{a+1}{2}$，
∴g（2）-g（$\frac{1}{2}$）≥$\frac{a+1}{2}$，解得a≥$\frac{4}{5}$，
∴$\frac{4}{5}$≤a＜1，
②当$\sqrt{\frac{1-a}{a}}≥2$时，$0＜a≤\frac{1}{5}$时，g（t）在$[{\frac{1}{2}，2}]$单调递减，
∵$g{（t）_{max}}-g{（t）_{min}}≥\frac{a+1}{2}$，
∴g（$\frac{1}{2}$）-g（2）≥$\frac{a+1}{2}$，解得a≤$\frac{2}{7}$，
∴$0＜a≤\frac{1}{5}$
③$\frac{1}{2}＜\sqrt{\frac{1-a}{a}}＜2，\frac{1}{5}＜a＜\frac{4}{5}$时，$g{（t）_{min}}=g（{\sqrt{\frac{1-a}{a}}}）$，最大值在$g（2）与g（{\frac{1}{2}}）$中取较大者，作差比较$g（2）-g（{\frac{1}{2}}）=3a-\frac{3}{2}＜0$，得到分类讨论标准：
（1）当$\frac{1}{5}＜a＜\frac{1}{2}$时，$g（2）-g（{\frac{1}{2}}）=3a-\frac{3}{2}＜0$，此时$g{（t）_{max}}=g（{\frac{1}{2}}）$
由$g{（t）_{max}}-g{（t）_{min}}≥\frac{a+1}{2}$
得到g（$\frac{1}{2}$）-g（$\sqrt{\frac{1-a}{a}}$）≥$\frac{a+1}{2}$，
∴32a²-40a+9≥0，解得a≥$\frac{5+\sqrt{7}}{8}$，或a≤$\frac{5-\sqrt{7}}{8}$
∴$\frac{1}{5}＜a≤\frac{{5-\sqrt{7}}}{8}$，
（2）当$\frac{1}{2}$≤a＜$\frac{4}{5}$时，g（$\frac{1}{2}$）-g（2）=3a-$\frac{3}{2}$＞0，此时g（t）_max=g（2），
由$g{（t）_{max}}-g{（t）_{min}}≥\frac{a+1}{2}$，
∴g（2）-g（$\sqrt{\frac{1-a}{a}}$）≥$\frac{a+1}{2}$，
∴a≥2$\sqrt{a（1-a）}$，解得a≥$\frac{4}{5}$，
∴此时a∈∅，
在此分类讨论中，a∈（0，$\frac{5-\sqrt{7}}{8}$]∪[$\frac{4}{5}$，1）
3当a≥1时，g（t）在t∈[$\frac{1}{2}$，2]上单调递增，
由$g{（t）_{max}}-g{（t）_{min}}≥\frac{a+1}{2}$，
∴g（2）-g（$\frac{1}{2}$）≥$\frac{a+1}{2}$，解得a≥$\frac{4}{5}$，
∴a≥1，
综上三大类情况，可得a的范围为（-∞，$\frac{5-\sqrt{7}}{8}$]∪[$\frac{4}{5}$，+∞）．

点评本题考查二次函数的图象和性质的运用，主要考查不等式恒成立问题，注意运用分类讨论和绝对值不等式的性质，考查运算能力，属于难题．