安徽省2024届同步达标自主练习·九年级第三次数学试卷答案,我们目前收集并整理关于安徽省2024届同步达标自主练习·九年级第三次数学得系列试题及其答案,更多试题答案请关注微信公众号:趣找答案/直接访问www.qzda.com(趣找答案)

安徽省2024届同步达标自主练习·九年级第三次数学试卷答案
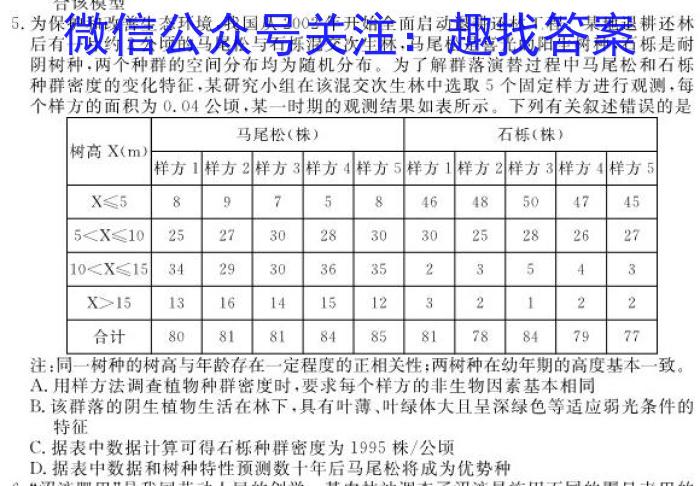
5.为保护和改善生态环境,我国从2002年开始全面启动退耕还林工程。某地退耕还林后有一片约2公顷的马尾松与石栎混交次生林,马尾松是喜光的阳生树种,石栎是耐阴树种,两个种群的空间分布均为随机分布。为了解群落演替过程中马尾松和石栎种群密度的变化特征,某研究小组在该混交次生林中选取5个固定样方进行观测,每个样方的面积为0.04公顷,某一时期的观测结果如表所示。下列有关叙述错误的是注:同一树种的树高与年龄存在一定程度的正相关性;两树种在幼年期的高度基本一致。A.用样方法调查植物种群密度时,要求每个样方的非生物因素基本相同B.该群落的阴生植物生活在林下,具有叶薄、叶绿体大且呈深绿色等适应弱光条件的特征C.据表中数据计算可得石栎种群密度为1995株/公顷D.据表中数据和树种特性预测数十年后马尾松将成为优势种
分析(1)设动点M的坐标为(x,y),根据动点M到点F(1,0)的距离比它到y轴的距离大1,建立方程,化简可得点M的轨迹C的方程;
(2)先根据抛物线方程求得焦点和准线方程,可把问题转化为P到准线与P到A点距离之和最小,进而根据抛物线的定义可知抛物线中P到准线的距离等于P到焦点的距离,进而推断出P、A、F三点共线时|PF|+|PA|距离之和最小,利用两点间距离公式求得|FA|,则|PA|+|PN|的最小值可求.
解答解:(1)设动点M的坐标为(x,y),
由题意,∵动点M到点F(1,0)的距离比它到y轴的距离大1,
∴$\sqrt{(x-1)^{2}+{y}^{2}}$=|x|+1;
化简得y2=4x(x≥0)或y=0(x≤0),
∴点M的轨迹C的方程为$\left\{\begin{array}{l}{{y}^{2}=4x(x≥0)}\\{y=0(x<0)}\end{array}\right.$;
(2)依题意可知,抛物线焦点为(1,0),准线方程为x=-1
只需直接考虑P到准线与P到A点距离之和最小即可,
由于在抛物线中P到准线的距离等于P到焦点的距离,
此时问题进一步转化为|PF|+|PA|距离之和最小即可(F为曲线焦点),
显然当P、A、F三点共线时|PF|+|PA|距离之和最小,为|FA|,
由两点间距离公式得|FA|=$\sqrt{(3-1)^{2}+(4-0)^{2}}$=2$\sqrt{5}$,
那么|PA|+|PN|的最小值为2$\sqrt{5}$-1.
点评本题考查轨迹方程,考查了直线与圆锥曲线的关系,考查了学生数形结合的思想和分析推理能力,是中档题.

