金考卷·百校联盟(新高考卷)2024年普通高等学校招生全国统一考试 预测卷(六七八)数学试卷答案,我们目前收集并整理关于金考卷·百校联盟(新高考卷)2024年普通高等学校招生全国统一考试 预测卷(六七八)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

金考卷·百校联盟(新高考卷)2024年普通高等学校招生全国统一考试 预测卷(六七八)数学试卷答案

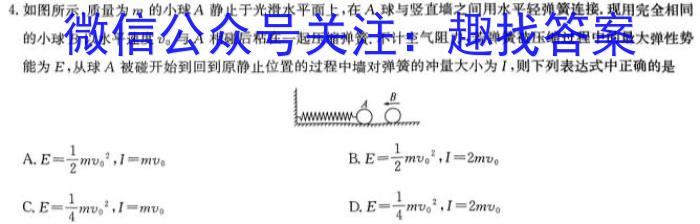
4.如图所示,质量为m的小球A静止于光滑水平面上,在A球与竖直墙之间用水平轻弹簧连接.现用完全相同的小球B以水平速度v0与A相碰后粘在一起压缩弹簧.不计空气阻力,若弹簧被压缩过程中的最大弹性势能为E,从球A被碰开始到回到原静止位置的过程中墙对弹簧的冲量大小为I,则下列表达式中正确的是A.E=12mv0^2,l=mv0B.E=12mv0^2,I=2mv0C.E=14mv0^2,I=mv0D.E=14mv0^2,I=2mv0

分析（1）根据正弦定理得出asinB=bsinA，从而求出sinA；
（2）先根据余弦定理求出边长a，再用中线长公式得出AD的长．

解答解：（1）根据正弦定理得，$\frac{a}{sinA}=\frac{b}{sinB}$，
所以，asinB=bsinA=2$\sqrt{3}$，
因为，b=4，所以，sinA=$\frac{\sqrt{3}}{2}$，
且三角形为锐角三角形，
所以，A=$\frac{π}{3}$；
（2）由（1）得，cosA=$\frac{1}{2}$，
根据余弦定理，a²=b²+c²-2bccosA，
所以，a²=4²+6²-2×4×6×$\frac{1}{2}$=28，
解得a=2$\sqrt{7}$，
因为D为BC的中点，则AD为BC边的中线，
因此，根据三角形中线长公式：
|AD|=m_a=$\frac{1}{2}$$\sqrt{2（b^2+c^2）-a^2}$=$\sqrt{19}$，
即线段AD的长度为$\sqrt{19}$．

点评本题主要考查了运用正弦定理和余弦定理解三角形，涉及三角形中线长的计算，属于中档题．