2026届普通高等学校招生统一考试青桐鸣高一12月大联考数学试卷答案,我们目前收集并整理关于2026届普通高等学校招生统一考试青桐鸣高一12月大联考数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

2026届普通高等学校招生统一考试青桐鸣高一12月大联考数学试卷答案

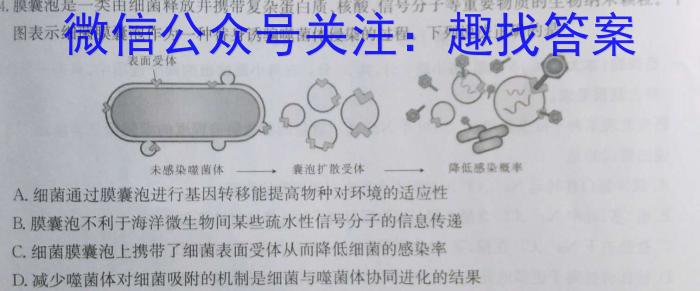
14.膜囊泡是一类由细菌释放并携带复杂蛋白质、核酸、信号分子等重要物质的生物纳米颗粒。下图表示细菌膜囊泡作为一种替身诱骗噬菌体侵染的过程。下列说法正确的是A.细菌通过膜囊泡进行基因转移能提高物种对环境的适应性B.膜囊泡不利于海洋微生物间某些疏水性信号分子的信息传递C.细菌膜囊泡上携带了细菌表面受体从而降低细菌的感染率D.减少噬菌体对细菌吸附的机制是细菌与噬菌体协同进化的结果

分析（1）根据向量数量积的定义求出函数f（x）的表达式，结合函数的对称性和最值之间的关系利用辅助角公式建立方程关系即可，求a，b的值；
（2）利用方程和函数之间的关系转化为两个函数的函数值相同问题，构造函数，利用三角函数的图象和性质求出函数的值域进行求解即可．

解答解：（1）∵f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$=2asinx+2bcosx，f（$\frac{π}{3}$）=2，
∴f（$\frac{π}{3}$）=$\sqrt{3}$a+b=2，
函数的导数f′（x）=2acosx-2bsinx，
∵导函数f′（x）的图象关于直线x=$\frac{5π}{6}$对称，
∴|-$\sqrt{3}$a-b|=$\sqrt{4{a}^{2}+4{b}^{2}}$=2，
即a²+b²=1，
∵$\sqrt{3}$a+b=2，
∴消去b得4a²-4$\sqrt{3}$a+3=0，
即（2a-$\sqrt{3}$）²=0，
则a=$\frac{\sqrt{3}}{2}$，b=$\frac{1}{2}$；
（2）∵a=$\frac{\sqrt{3}}{2}$，b=$\frac{1}{2}$；
∴f（x）=$\sqrt{3}$sinx+cosx=2sin（x+$\frac{π}{3}$），
若关于x的方程f（x）+log₂k=0在区间[0，$\frac{π}{2}$]上总有实数解，
则等价为log₂k=-f（x）=-2sin（x+$\frac{π}{3}$）在区间[0，$\frac{π}{2}$]上总有实数解，
设g（x）=）=-2sin（x+$\frac{π}{3}$），
当0≤x≤$\frac{π}{2}$时，$\frac{π}{3}$≤x+$\frac{π}{3}$≤$\frac{5π}{6}$，
则$\frac{1}{2}$≤sin（x+$\frac{π}{3}$）≤1，
则-2≤-2sin（x+$\frac{π}{3}$）≤-1，
由-2≤log₂k≤-1，
解得$\frac{1}{4}$≤k≤$\frac{1}{2}$．

点评本题主要考查函数与方程的应用，利用三角函数的辅助角公式将函数进行化简是解决本题的关键．综合性较强，运算量较大．