山东省济南市2023-2024学年高一年级上学期1月期末考试数学试卷答案,我们目前收集并整理关于山东省济南市2023-2024学年高一年级上学期1月期末考试数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

山东省济南市2023-2024学年高一年级上学期1月期末考试数学试卷答案

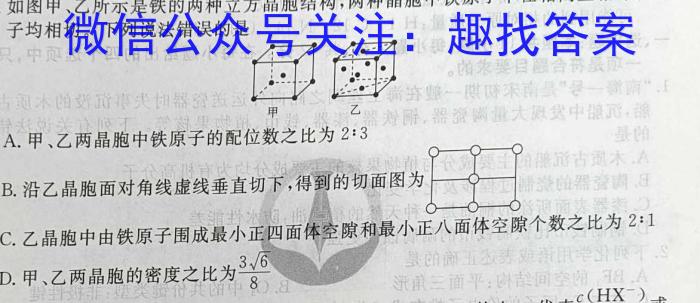
13.如图甲、乙所示是铁的两种立方晶胞结构,两种晶胞中铁原子半径相同且相邻铁原子均相切。下列说法错误的是只,中页赶个四!A.甲、乙两晶胞中铁原子的配位数之比为2:3B.沿乙晶胞面对角线虚线垂直切下,得到的切面图为C.乙晶胞中由铁原子围成最小正四面体空隙和最小正八面体空隙个数之比为2:1D.甲、乙两晶胞的密度之比为为3

分析（1）函数f（x）=$\frac{{e}^{x}+b}{{e}^{x}}$=1+$\frac{b}{{e}^{x}}$，f′（x）=-$\frac{b}{{e}^{-x}}$．利用f′（0）=-b=1，解得b．可得f（x）=1-$\frac{1}{{e}^{x}}$，要证明当x＞-1时，f（x）≥$\frac{x}{x+1}$，即证明e^x≥x+1，令g（x）=e^x-x-1，（x＞-1）．利用当时研究其单调性极值即可得出．
（2）当x≥0时，不等式0≤f（x）=$1-\frac{1}{{e}^{x}}$≤$\frac{x}{ax+1}$，当x≥0，1-e^-x∈[0，1），可得$\frac{x}{ax+1}$≥0，必须a≥0．于是不等式$1-\frac{1}{{e}^{x}}$≤$\frac{x}{ax+1}$恒成立?（ax+1）（1-e^-x）-x≤0在[0，+∞）上恒成立．令u（x）=（ax+1）（1-e^-x）-x，则u′（x）=a（1-e^-x）+（ax+1）e^-x-1，令v（x）=a（1-e^-x）+（ax+1）e^-x-1，v′（x）=e^-x（2a-ax-1）．对a分类讨论：当a=0时，容易验证．当a＞0时，v′（x）=-ae^-x$（x-\frac{2a-1}{a}）$．对a分类讨论：i）若2a-1≤0，即$0＜a≤\frac{1}{2}$时，v′（x）≤0，即可得出ii）若2a-1＞0，即a$＞\frac{1}{2}$时，当$0＜x＜\frac{2a-1}{a}$时，v′（x）＞0舍去．

解答（1）证明：∵f（x）在点（0，f（0））处的切线为x-y=0．可知：切线的斜率为1．
函数f（x）=$\frac{{e}^{x}+b}{{e}^{x}}$=1+$\frac{b}{{e}^{x}}$，f′（x）=-$\frac{b}{{e}^{-x}}$．
∴f′（0）=-b=1，解得b=-1．
∴f（x）=1-$\frac{1}{{e}^{x}}$，
要证明当x＞-1时，f（x）≥$\frac{x}{x+1}$，即证明e^x≥x+1，
令g（x）=e^x-x-1，（x＞-1）．
g′（x）=e^x-1，
当x＞0时，g′（x）＞0，此时函数g（x）单调递增；当0＞x＞-1时，g′（x）＜0，此时函数g（x）单调递减．
∴当x=0时，函数g（x）取得极小值即最小值，g（0）=0，
∴g（x）≥0，
∴e^x≥x+1．
（2）解：当x≥0时，不等式0≤f（x）=$1-\frac{1}{{e}^{x}}$≤$\frac{x}{ax+1}$，
∵x≥0，1-e^-x∈[0，1），∴$\frac{x}{ax+1}$≥0，
若x=0，则a∈R．若x＞0，则ax+1＞0，即a＞-$\frac{1}{x}$恒成立，则a≥0．
于是不等式$1-\frac{1}{{e}^{x}}$≤$\frac{x}{ax+1}$恒成立?（ax+1）（1-e^-x）-x≤0在[0，+∞）上恒成立．
令u（x）=（ax+1）（1-e^-x）-x，u（0）=0，则u′（x）=a（1-e^-x）+（ax+1）e^-x-1，
令v（x）=a（1-e^-x）+（ax+1）e^-x-1，v′（x）=e^-x（2a-ax-1），v（0）=0．
①当a=0时，v′（x）=-e^-x＜0，∴v（x）=u′（x）≤v（0）=0．
∴u（x）在[0，+∞）上单调递减，∴u（x）≤u（0）=0，∴f（x）≤g（x）在[0，+∞）上恒成立．
②当a＞0时，v′（x）=-ae^-x$（x-\frac{2a-1}{a}）$．
i）若2a-1≤0，即$0＜a≤\frac{1}{2}$时，v′（x）≤0，∴v（x）=u′（x）≤v（0）=0．
∴u（x）在[0，+∞）上单调递减，∴u（x）≤u（0）=0，∴f（x）≤g（x）在[0，+∞）上恒成立．
ii）若2a-1＞0，即a$＞\frac{1}{2}$时，当$0＜x＜\frac{2a-1}{a}$时，v′（x）＞0，∴v（x）在$（0，\frac{2a-1}{a}）$上单调递减，
∴v（x）=u′（x）＞v（0）=0．
∴u（x）在$（0，\frac{2a-1}{a}）$上单调递增，∴u（x）＞u（0）=0，∴f（x）＞g（x），不满足条件，舍去．
综上可得：当x≥0时，f（x）≤$\frac{x}{ax+1}$恒成立的实数a的取值范围是$[0，\frac{1}{2}]$．

点评本题考查了利用导数研究其单调性极值与最值、恒成立问题等价转化方法，考查了分类讨论方法、推理能力与计算能力，属于难题．