智学大联考·皖中名校联盟2023-2024学年（上）高一第四次联考数学试卷答案,我们目前收集并整理关于智学大联考·皖中名校联盟2023-2024学年（上）高一第四次联考数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

智学大联考·皖中名校联盟2023-2024学年（上）高一第四次联考数学试卷答案

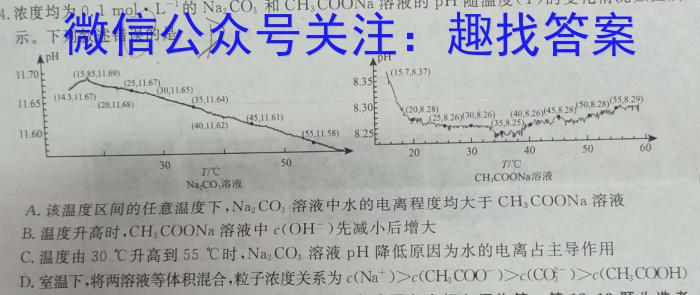
14.浓度均为0.1molL^-1的Na2CO3和CH3COONa溶液的pH随温度(T)的变化情况如图所A.该温度区间的任意温度下,Na2CO3溶液中水的电离程度均大于CH3COONa溶液B.温度升高时,CH3COONa溶液中c(OH^-)先减小后增大C.温度由30^C升高到55^C时,Na2CO3溶液pH降低原因为水的电离占主导作用D.室温下,将两溶液等体积混合,粒子浓度关系为c(Na^+)>c(CH3COO^-)>c(CO3^2-)>c(CH3COOH)

分析构造函数f（x）=sinx，由f′（x）在（0，π）上是减函数，得出存在点ξ∈（x₁，x₂），使f′（ξ）=$\frac{si{nx}_{1}-si{nx}_{2}}{{x}_{1}{-x}_{2}}$；
η∈（x₂，x₃），使f′（η）=$\frac{si{nx}_{2}-si{nx}_{3}}{{x}_{2}{-x}_{3}}$，再由f′（x）的递减性即得所证．

解答证明：设函数f（x）=sinx，则f′（x）=cosx在（0，π）上是减函数；
∵f（x）在（x₁，x₂）上可导，在[x₁，x₂]上连续，
∴由拉格朗日中值定理知，
存在一点ξ∈（x₁，x₂），使得f′（ξ）=$\frac{si{nx}_{1}-si{nx}_{2}}{{x}_{1}{-x}_{2}}$；
同理，存在一点η∈（x₂，x₃），使得f′（η）=$\frac{si{nx}_{2}-si{nx}_{3}}{{x}_{2}{-x}_{3}}$；
又ξ＜η，利用f′（x）的递减性知，
f′（ξ）＞f′（η），
∴$\frac{sin{x}_{1}-sin{x}_{2}}{{x}_{1}-{x}_{2}}$＞$\frac{sin{x}_{2}-sin{x}_{3}}{{x}_{2}-{x}_{3}}$．

点评本题考查了利用函数的导数证明不等式的问题，也考查了转化思想的应用问题，是较难的题目．