安徽省2023-2024学年八年级上学期综合评估（1月）数学试卷答案,我们目前收集并整理关于安徽省2023-2024学年八年级上学期综合评估（1月）数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

安徽省2023-2024学年八年级上学期综合评估（1月）数学试卷答案

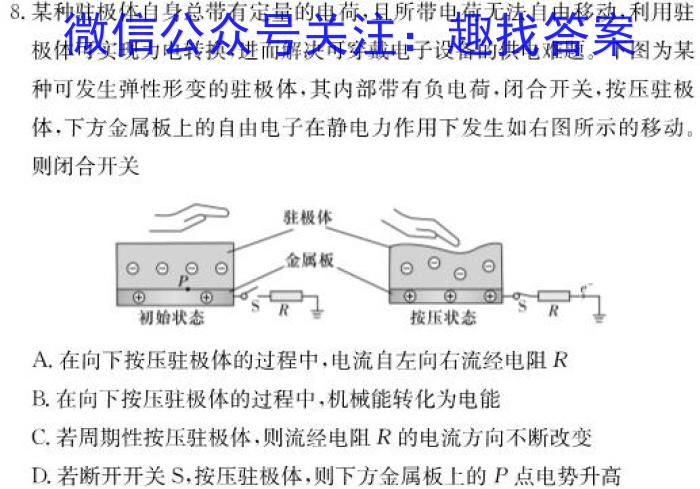
8.某种驻极体自身总带有定量的电荷,且所带电荷无法自由移动,利用驻极体可实现力电转换,进而解决可穿戴电子设备的供电难题。下图为某种可发生弹性形变的驻极体,其内部带有负电荷,闭合开关,按压驻极体,下方金属板上的自由电子在静电力作用下发生如右图所示的移动。则闭合开关A.在向下按压驻极体的过程中,电流自左向右流经电阻RB.在向下按压驻极体的过程中,机械能转化为电能C.若周期性按压驻极体,则流经电阻R的电流方向不断改变D.若断开开关S,按压驻极体,则下方金属板上的P点电势升高

分析化简f（x）=x³-$\frac{3}{4}$x+$\frac{1}{4}$，求导f′（x）=3x²-$\frac{3}{4}$，设切点坐标为（x₀，f（x₀）），从而可得0-（x₀³-$\frac{3}{4}$x₀+$\frac{1}{4}$）=（3x₀²-$\frac{3}{4}$）（0-x₀），从而解得．

解答解：当a=-$\frac{3}{4}$时，f（x）=x³-$\frac{3}{4}$x+$\frac{1}{4}$，
f′（x）=3x²-$\frac{3}{4}$，
设切点坐标为（x₀，f（x₀）），
故切线方程为y-（x₀³-$\frac{3}{4}$x₀+$\frac{1}{4}$）=（3x₀²-$\frac{3}{4}$）（x-x₀），
∵过点（0，0），
∴0-（x₀³-$\frac{3}{4}$x₀+$\frac{1}{4}$）=（3x₀²-$\frac{3}{4}$）（0-x₀），
解得，x₀=$\frac{1}{2}$，
故过点（0，0）与曲线y=f（x）相切的直线方程为
y-（$\frac{1}{8}$-$\frac{3}{8}$+$\frac{1}{4}$）=（3•$\frac{1}{4}$-$\frac{3}{4}$）（x-$\frac{1}{2}$），即y=0．

点评本题考查了导数的几何意义的应用及切线的求法．