启光教育 2023-2024学年度七年级第一学期期末学业质量监测(2024.1)数学试卷答案,我们目前收集并整理关于启光教育 2023-2024学年度七年级第一学期期末学业质量监测(2024.1)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

启光教育 2023-2024学年度七年级第一学期期末学业质量监测(2024.1)数学试卷答案

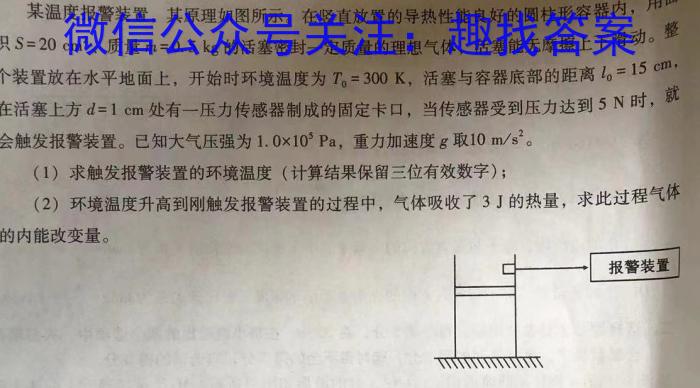
某温度报警装置,其原理如图所示。在竖直放置的导热性能良好的圆柱形容器内,积S=20cm^2、m=0.5kgS=20cm、质量m=0.5kg的活塞密封一定质量的理想气体,活塞能无摩擦上下滑动。。整个装置放在水平地面上,开始时环境温度为T=300K,活塞与容器底部的距离l,=15cT0=300K,l0=15cm,cm,d=1cm在活塞上方d=1cm处有一压力传感器制成的固定卡口,当传感器受到压力达到5N时,就会触发报警装置。已知大气压强为1.010^5Pa,,重力加速度g取10m/s^2。(1)求触发报警装置的环境温度(计算结果保留三位有效数字);(2)环境温度升高到刚触发报警装置的过程中,气体吸收了3J的热量,求此过程气体的内能改变量。报警装置

分析先根据条件得出函数在（0，4]上的解析式f（x）$\left\{\begin{array}{l}{2-x，0＜x＜1}\\{2^x-1，1≤x≤4}\end{array}\right.$，再运用分类讨论和数形结合的方法确定零点和m的范围．

解答解：根据定义，当x∈（0，4]时，f（x）=max{2^x-1，2-x}=$\left\{\begin{array}{l}{2-x，0＜x＜1}\\{2^x-1，1≤x≤4}\end{array}\right.$，
方程f（x）-mx²+1=0化为f（x）=mx²-1，记g（x）=mx²-1，分类讨论如下：
①当m＞0时，g（x）的图象为开口向上的抛物线，
根据几何关系，g（x）的图象只与f（x）图象在y轴右边有公共点，如下图：
根据题意，方程：2^x-1=mx²-1在（1，4]有两个交点，
分离参数得，m=$\frac{2^x}{x^2}$=h（x），令h'（x）=$\frac{2^x（xln2-2）}{x^3}$=0，解得x=$\frac{2}{ln2}$∈（2，3），
显然，当x=$\frac{2}{ln2}$时，h（x）_min=h（$\frac{2}{ln2}$）=$\frac{e^2ln^22}{4}$，且h（1）=2，h（2）=1，
要使原方程有两个实根，则$\frac{e^2ln^22}{4}$＜m≤1；
几何意义：m=$\frac{e^2ln^22}{4}$时，两图象相切；m=1时，g（x）图象过点（4，15）．
②当m＜0时，g（x）的图象为开口向下的抛物线，
根据几何关系，g（x）的图象只与f（x）图象在y轴左边有公共点，
即方程f（x）-mx²+1=0在[-4，0）恰有两根，
若x=-4为方程的根，则f（-4）-16m+1=0，解得m=-$\frac{7}{8}$，
所以，由图可知，m∈[-$\frac{7}{8}$，0），
综合以上讨论得，m∈[-$\frac{7}{8}$，0）∪（$\frac{e^2ln^22}{4}$，1]，
故选：A．

点评本题主要考查了函数零点的判定，涉及奇函数与分段函数的图象与性质，运用了换元法，分离参数法和数形结合的解题思想，属于难题．