学林教育 2023~2024学年度九年级全年教学质量检测试题(卷)数学试卷答案,我们目前收集并整理关于学林教育 2023~2024学年度九年级全年教学质量检测试题(卷)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

学林教育 2023~2024学年度九年级全年教学质量检测试题(卷)数学试卷答案

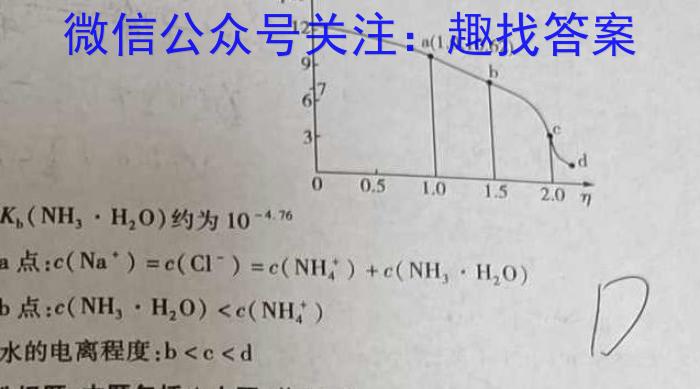
A.Kb(NH3H2O)约为10^-4.76B.a点:c(Na^+)=c(Cl^-)=c(NH4^+)+c(NH3H2O)C.b点:c(NH,·H,0)

分析（1）利用递推关系与等比数列的通项公式即可得出；
（2）利用对数的运算性质、等差数列的定义、通项公式及其前n项和公式可得S_n，进而解出不等式．

解答解：（1）当n=1时，S₁=a₁=2+a≠0，
当n≥2时，${a_n}={S_n}-{S_{n-1}}={2^{n-1}}$，
∵{a_n}是等比数列，
∴${a_1}=2+a={2^{1-1}}=1$，即a₁=1，a=-1，
∴数列{a_n}的通项公式我${a_n}={2^{n-1}}$（n∈N^*）．
（2）由（1）得${b_n}={log_4}{a_n}+1=\frac{n+1}{2}$，
∵${b_{n+1}}-{b_n}=\frac{n+2}{2}-\frac{n+1}{2}=\frac{1}{2}$，
∴数列{b_n}是首项为1，公差为$d=\frac{1}{2}$的等差数列，
∴${S_n}=n{b_1}+\frac{{n（{n-1}）}}{2}d=\frac{{{n^2}+3n}}{4}$．
由2S_n≤5得n²+3n-10≤0，即-5≤n≤2，
又n∈N^*，∴所求不等式的解集为{1，2}．

点评本题考查了递推关系、等比数列的通项公式、对数的运算性质、等差数列的定义通项公式及其前n项和公式、不等式的解法，考查了推理能力与计算能力，属于中档题．